According to the official rules of Monopoly, landing on the Free Parking space results in no action, however, many house rules include some sort of financial reward for landing on this space. For instance, I have always collected everything paid to “The Bank” through Chance/Community Chest cards, the Luxury Tax space, and Income Tax space to give to the lucky one who hits Free Parking.
In any event, let’s find out how many rolls it takes to get there. Since Monopoly is state-based and no result of any roll depends on what happened on the previous roll (with one exception we’ll note, but not address, later), we get to apply a Markov model to our Monopoly board. This means we can create a matrix where the rows and columns represent spaces on the board, and the value of row i, column j, is the probability of reaching space j from space i after one roll of the dice. For those not interested in the calculations, you can skip to the graph below.
There are 40 spaces on the board, so we start with a 40×40 matrix, where each roll gets us at least two spaces from our current position, but no more than twelve. For instance, row 26 represents the case where one’s token rests on B&O Railroad. The corresponding row in the transition matrix is shown below.
Of course, the critical reader will note that column 31 represents the “Go Directly To Jail” space, so we cannot actually land on it! Since a roll of five would actually land us in jail (space 11), we simply move the 1/9 in column 31 to column 11, and do the same for every roll which can land on space 31 with non-zero probability.
Unfortunately, this is not the only jump space, and in fact, it’s the easiest one to handle. The other jump spaces are the Chance and Community Chest cards, which only jump when certain cards are drawn, and worse, in some cases jump to different squares when drawn from different Chance or CC locations. And worse still, in the most awful case for which to account, space 37 (Chance) might send us back to space 34 (Community Chest) which might then send us to either space 1 (Go!) or Space 11 (Jail)!
I’m going to simply start with Chance spaces, and justify that choice later. In the game I use, we have fifteen Chance cards, 9 of which cause a jump, so the probability of jumping from any of the Chance spaces (8, 23, and 37) is 9 out of 15. The jump spaces are as follows:
- Back three space
- Go (1)
- Illinois Avenue (25)
- St. Charles Place (12)
- Jail (11)
- Reading Railroad (6)
- Boardwalk (40)
- Nearest Utility: 8, 37 -> Electric Company (13); 23-> Water Works (29)
- Nearest Railroad: 8->Pennsylvania (16); 23->B&O (26); 37->Reading (6)
- Go! (1)
- Jail (11)
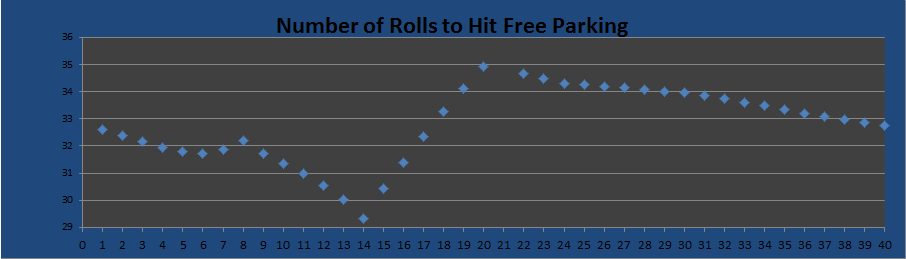
- First, the low point of the graph is position 14, Virginia Avenue, corresponding to a little over 29 rolls, on average, to reach Free Parking. This shouldn’t be surprising since fully one-sixth of the time, it will happen by simply rolling a seven. This does suggest that the numbers on the dice outweigh the effect of the many warps on the board.
- Next, position 21 is missing. That’s because it’s Free Parking, and the data point is actually off the chart (at zero).
- The high point, at around 35 rolls, is position 20, New York Avenue. There is a steady march upwards from Virginia Avenue to New York Avenue precisely because more and more dice rolls send you past the desired space.
- The “V” in the graph before the Free Parking space further reinforces the fact that getting to Free Parking is easiest when you are sitting right next to it, and the minimal number of warp spaces in that region makes the graph fairly linear.
- The local minimum at Reading Railroad (6) interests me, but I don’t have a very good guess about why it exists there. It’s possible that rolling a total of 15 over the course of a few rolls is just more likely than 16 or 14. I haven’t done the calculations.
Notes:
There is one thing we haven’t considered: Rolling three doubles in a row will land you in jail! I haven’t considered this case for a very good reason; I don’t feel like it. To include it in the transition matrix would require “remembering” how many doubles had been rolled to reach the current state, but this goes against everything a transition matrix stands for. It’s possible that simply giving each roll a 1/216 (the chance of rolling three doubles in a row) probability of landing on jail would solve the problem, but I haven’t considered it fully and I think that logic might be deficient.
For those interested in the mechanics of manipulating the matrices, I actually used an old copy of Maple 8 for the calculations. The operation of taking the inverse of a 39×39 matrix took more than a few seconds, but Maple and my dual-core laptop were up to the task. If you have a copy of Maple and would like to peruse the worksheet yourself, please feel free.
I also haven’t considered the fact that once a Chance or Community Chest card is drawn, it cannot be drawn again, however, since we’re looking at long term probabilities and the cards are in fact reshuffled after all of them have been exhausted, this is an acceptable model.
Conclusion:
I don’t really know how long the average Monopoly game lasts, but it takes quite some time to reach that Free Parking space, so make your investments wisely because it will not likely be your savior. It takes quite some time to get there. It might also be interesting to find out how long one has to wait to get to some of the warped spaces, for instance, Jail, but I’ll leave that discussion (and any conclusions about modern society) for another entry.